¿Cómo calcular THD y PF?

¿Cómo calcular THD y PF?

 

Análisis de distorsión armónica total (THD) y evaluación del factor de potencia En esta discusión, exploraremos metodologías para medir la distorsión armónica total junto con cálculos del factor de potencia.

La distorsión armónica total (THD) es una métrica que refleja la combinación de frecuencias armónicas yuxtapuestas a la frecuencia primaria, como 60 Hz, en un circuito. Abarca todas las frecuencias armónicas presentes. THD puede estar asociado con armónicos de corriente o voltaje. Para cuantificar la distorsión en el voltaje de línea, aplique la siguiente fórmula:

 

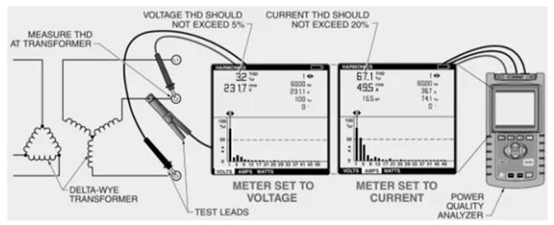
Figura 1. La medición de THD debe realizarse en el transformador, no adyacente a la carga.

Donde Vn_rms es el voltaje RMS del enésimo armónico y Vfund_rms denota el voltaje RMS de la frecuencia fundamental. Una onda sinusoidal pura, desprovista de armónicos superiores, como una fuente de tensión impecable, presenta un THD del 0%. Cualquier valor de THD superior a cero indica distorsión de la onda sinusoidal. Las cifras de THD normalmente se presentan como porcentajes, por ejemplo, 5% o 50%. La THD se puede evaluar tanto para señales de corriente como de voltaje.

Las corrientes armónicas surgen de cargas no lineales que consumen corriente en pulsos. Los armónicos de voltaje surgen de estas corrientes que atraviesan diversas resistencias del sistema. La corriente del transformador induce una caída de voltaje en sus bobinas. Cuando se pulsa la corriente, el voltaje refleja esta pulsación. La distorsión excesiva de la tensión es perjudicial ya que sirve como conducto de los armónicos hacia cargas lineales, como los motores eléctricos. Los armónicos de voltaje introducen calentamiento adicional en los sistemas de distribución de energía y los dispositivos conectados.

 

Medición de THD

Al solucionar problemas de circuitos por armónicos, asegúrese de medir tanto el THD de voltaje como el THD de corriente. Los resultados ideales garantizan que la THD del voltaje no supere el 5 % y que la THD actual permanezca por debajo del 20 % de la frecuencia base. La THD debe evaluarse a nivel del transformador para un cálculo preciso de la THD en todo el sistema (como se muestra en la Ilustración 1). Las lecturas de THD del lado de carga ofrecen los valores más elevados ya que no se ha producido cancelación de armónicos en todo el sistema.

 

Cuando se mide la corriente THD en condiciones de carga completa, el THD es similar a la distorsión de demanda total (TDD). TDD es el cociente de los armónicos actuales a la corriente de carga última. Se ejecuta una medición de THD al diagnosticar o probar sistemas. TDD difiere de THD porque TDD se compara con la medición de corriente máxima a lo largo del tiempo. THD únicamente mide la corriente en el instante de la medición. La función de TDD es tener en cuenta los casos en los que el THD es elevado, pero la carga agregada es relativamente baja. En tales circunstancias, el TDD es modesto y minimiza el sobrecalentamiento.

 

Factor de potencia

 

Power factor delineates the ratio of authentic power to apparent power in a circuit or distribution network. Every AC circuit is comprised of real, reactive, harmonic, and apparent (aggregate) power. True power, in watts or kilowatts, is expended by motors, lighting, and other apparatuses to execute functional tasks. Reactive power, in volt-amperes reactive or kilovolt-amperes reactive, is stored and discharged by inductors and capacitors. Reactive power materializes as phase displacement between current and voltage waveforms. Harmonic power, in volt-amperes or kilovolt-amperes, is dissipated due to harmonic distortion. Apparent power, in volt-amperes or kilovolt-amperes, is the vectorial sum of true power, reactive power, and harmonic power. Apparent power isn't a simple accumulation but a vector summation.

 

Displacement Power Factor

 

The displacement power factor is the ratio of genuine power to apparent power attributable to phase displacement between current and voltage (as shown in Illustration 2). Capacitors can frequently be integrated into a circuit or distribution network to rectify the displacement power factor. Its computation is as follows:

PF = cos(θ)

where PF signifies displacement power factor and θ is the discrepancy between voltage and current phases in degrees. Note: DPF or PFD may occasionally substitute PF to denote displacement power factor.

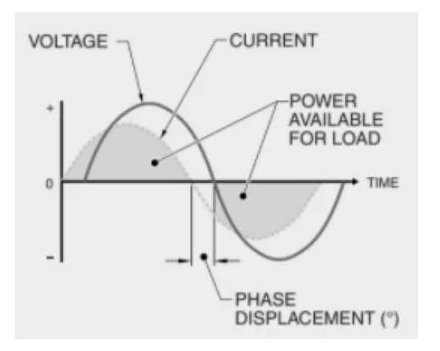
Figure 2. Displacement power factor enables calculation of the power genuinely accessible for a load.

 

 

The presence of harmonics introduces complexity into the discussion of power factor. The distortion power factor, defined as the ratio of true power to apparent power due to Total Harmonic Distortion (THD), cannot be mitigated simply by adding capacitors to a circuit. This is because the impedance of capacitors decreases with an increase in frequency, potentially turning them into sinks for high-frequency harmonics rather than effective compensators.

 

To address the distortion power factor, specialized solutions are employed. These include special types of transformers designed to handle harmonic loads or tuned harmonic filters that consist of a combination of capacitors and inductors. Such filters are specifically engineered to resonate at harmonic frequencies, effectively absorbing or cancelling out these distortions.

 

The calculation of the distortion power factor involves assessing the impact of harmonic content on the overall power factor, reflecting the diminished efficiency caused by the presence of these higher-order frequencies in the electrical system.

The distortion power factor is calculated as follows:

.

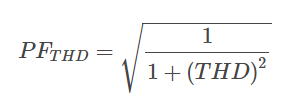
where
PFTHD = distortion power factor
THD = total harmonic distortion

The total power factor is the product of the displacement power factor and the distortion power factor and is calculated as follows:

PFTot = PF × PFTHD

where
PFTot = total power factor
PF = displacement power factor
PFTHD = distortion power factor

For example, what is the total power factor when the displacement between voltage and current is 25°, and the THD is 49% (0.49)? The displacement power factor is calculated as follows:

PF = cos(θ)
PF = cos (25°)
PF = 0.906

The distortion power factor is calculated as follows:

.

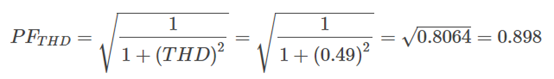The total power factor is calculated as follows:

PFTot = PF × PFTHD
PFTot = 0.906 × 0.898
PFTot = 0.814

Understanding the total power factor is crucial as it directly correlates with apparent power, which is fundamental in sizing components within a power distribution system. Apparent power serves as a key metric for ensuring that all elements in the system are appropriately rated to handle the electrical load without being overloaded.

 

Current Crest Factor

 

The current crest factor, defined as the ratio of the waveform's peak value to its RMS value, serves to indicate the extent of distortion in the waveform. Its calculation provides insights into the waveform's quality, with higher factors pointing to greater levels of distortion. The formula for determining the current crest factor is as follows:

.

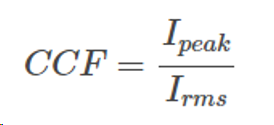where
CCF = current crest factor
Ipeak = peak value (in A)
Irms = root mean square value (in A)

For example, what is the current crest value of a perfect sine waveform? In a perfect sine waveform with a peak value of 1, the rms value is 0.707.

.

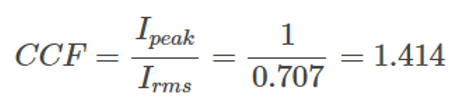An elevated current crest factor can result in excessive heat generation within circuits and devices. For instance, on a 120V circuit powering digital equipment such as computers, a distorted current waveform might display a crest factor ranging from 2 to 6 (consult Figure 3). Typically, circuits with a higher current crest factor contain a greater proportion of energy in their higher harmonics.

 

A power source is obligated to provide the peak power needed by the circuit, matching the specified voltage and current demands. A conventional backup power system, such as an uninterruptible power supply for computers, is capable of delivering a current crest factor of 3 when operating at full capacity but may experience augmented crest factors under lighter load conditions.

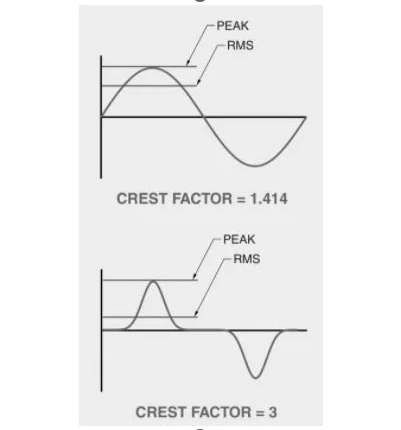
Figure 3. The current crest factor comparison

 

 Source Impedance

 

La impedancia de la fuente afecta el factor de cresta generado por cargas no lineales. Al alcanzar un umbral de voltaje específico, la fuente de alimentación inicia la carga de un condensador de suavizado. Cuando la impedancia de la fuente es mínima, el aumento de corriente en el capacitor es sustancial, lo que resulta en una breve duración de carga. Por el contrario, una impedancia más alta limita el flujo de corriente, alargando así el período de carga del condensador. Este intervalo de carga prolongado disminuye efectivamente el factor de cresta. Se puede aumentar la impedancia de la fuente mediante la incorporación de reactores de línea o accionar transformadores de aislamiento.